Insana Lab: Ultrasonic Imaging - The University of Illinois at Urbana-Champaign
Project 1: Elasticity Imaging of Breast Cancer
5.5.05
 1.A. Imaging Basics
1.A. Imaging BasicsFig 1. Elasticity Imaging is a diagnostic technique for noninvasive visualization of soft tissue stiffness. Elasticity imaging can detect disease processes involving local inflammatory responses, which can be acute or chronic and associated with fibrosis, hyperplasia, and neoplasia. Elasticity methods is also palpation (Fig 1), however in place of the fingers standard imaging methods are used to remotely sense the deformation patterns resulting from an applied force. The advantage over manual palpation is high depth resolution and increase sensitivity to deep lesions. The term "elasticity imaging" encompasses a large range of techniques, although many are based on imaging deformation or strain. |
|
 Fig 2.
Static strain imaging: Any medical imaging method can be used to
sense deformation patterns, although those employing phase-sensitive
detection – ultrasound (Fig 2), MRI, optical – have the greatest
sensitivity to the tiny displacements (10-9 – 10-6 m) associated with
elasticity imaging. The basic method for static strain imaging is simple:
scan the medium and record the radio-frequency (RF) echoes normally used to
make an ultrasound image for some region of interest (boxed region in
meshed images). Then apply a small deforming stress at the surface and
scan the region again. The two echo fields are "compared" to estimate the
displacement of local structures. The spatial derivative of estimated
displacement in the direction of the beam axis (vertically in this example)
is the strain tenor we estimate. As shown in Fig. 2, finite-element
methods are used to model the deformation, which are then validated using
phantom experiments (lower right).
Fig 2.
Static strain imaging: Any medical imaging method can be used to
sense deformation patterns, although those employing phase-sensitive
detection – ultrasound (Fig 2), MRI, optical – have the greatest
sensitivity to the tiny displacements (10-9 – 10-6 m) associated with
elasticity imaging. The basic method for static strain imaging is simple:
scan the medium and record the radio-frequency (RF) echoes normally used to
make an ultrasound image for some region of interest (boxed region in
meshed images). Then apply a small deforming stress at the surface and
scan the region again. The two echo fields are "compared" to estimate the
displacement of local structures. The spatial derivative of estimated
displacement in the direction of the beam axis (vertically in this example)
is the strain tenor we estimate. As shown in Fig. 2, finite-element
methods are used to model the deformation, which are then validated using
phantom experiments (lower right).
|
|
 Fig 3.
The strategy for elasticity imaging is to compress the tissue surface by a distance equal to
0.5 – 5% of the total tissue thickness. The compression should be applied to keep as much
of the tissue motion in the imaging plane of the ultrasound transducer as possible
(plane-strain deformation). Movements outside the scan plane cannot be tracked because
of echo decorrelation, and thus decorrelation noise is produced. There are several
conditions that decorrelate echoes. If the local elastic modulus of the medium does
not vary significantly from the mean value (low dynamic range for strain) then compressions
up to 5% are possible with minimal decorrelation noise, Fig 3.
Fig 3.
The strategy for elasticity imaging is to compress the tissue surface by a distance equal to
0.5 – 5% of the total tissue thickness. The compression should be applied to keep as much
of the tissue motion in the imaging plane of the ultrasound transducer as possible
(plane-strain deformation). Movements outside the scan plane cannot be tracked because
of echo decorrelation, and thus decorrelation noise is produced. There are several
conditions that decorrelate echoes. If the local elastic modulus of the medium does
not vary significantly from the mean value (low dynamic range for strain) then compressions
up to 5% are possible with minimal decorrelation noise, Fig 3.
|
|
 Fig 4.
Media with high dynamic range for stiffness are often encountered in clinical practice.
The flow phantom in Fig 4 illustrates the point. Using the multi-resolution
cross-correlation (MRCC) algorithm originally developed by Pawan Chaturvedi [1,2], we obtain high
contrast and spatial resolution but suffer decorrelation noise near regions of large elasticity contrast.
If decorrelation can be avoided, the MRCC algorithm is the maximum likelihood estimator of strain [3].
However, when the associated MLE assumptions are violated, then algorithms that regularize solutions are
sought. A multi-scale, regularized strain estimator based on the optical flow approach was used to
reprocess the flow phantom echo data on the right side of Fig 4. This was developed by Claire Pellot-Barakat
in collaboration with investigators from INSERM in Paris [4]. There is some loss of contrast and spatial
resolution with this optical flow (OF) algorithm [5], but the large reduction in noise has led us to adopt
it for all our clinical studies
Fig 4.
Media with high dynamic range for stiffness are often encountered in clinical practice.
The flow phantom in Fig 4 illustrates the point. Using the multi-resolution
cross-correlation (MRCC) algorithm originally developed by Pawan Chaturvedi [1,2], we obtain high
contrast and spatial resolution but suffer decorrelation noise near regions of large elasticity contrast.
If decorrelation can be avoided, the MRCC algorithm is the maximum likelihood estimator of strain [3].
However, when the associated MLE assumptions are violated, then algorithms that regularize solutions are
sought. A multi-scale, regularized strain estimator based on the optical flow approach was used to
reprocess the flow phantom echo data on the right side of Fig 4. This was developed by Claire Pellot-Barakat
in collaboration with investigators from INSERM in Paris [4]. There is some loss of contrast and spatial
resolution with this optical flow (OF) algorithm [5], but the large reduction in noise has led us to adopt
it for all our clinical studies
|
|
 Fig 5.
Time-varying strain imaging: As shown in Fig 5, we often apply a step stress field (in reality
it is a short-time ramp stress that is held constant with time). If we acquire RF echo frames
shortly before and after applying a small step stress, then the strain image that results is
from the incompressible phase of the deformation process. That is, not enough time has passed
for any of the viscous mechanisms to engage, so the medium reacts as if it were incompressible
(
Fig 5.
Time-varying strain imaging: As shown in Fig 5, we often apply a step stress field (in reality
it is a short-time ramp stress that is held constant with time). If we acquire RF echo frames
shortly before and after applying a small step stress, then the strain image that results is
from the incompressible phase of the deformation process. That is, not enough time has passed
for any of the viscous mechanisms to engage, so the medium reacts as if it were incompressible
(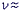 0.5) and elastic. Small applied stresses ensure that the stress-strain curve is linear.
However if we hold the stress constant longer than a few seconds, we see that the strain
increases slowly over time (see plots in Fig 5). Whether we are imaging water-based gelatin
or breast tissue, it seems there are two physical mechanisms behind the mechanical relaxation.
These are related to fluid flow (poroelasticity) and cross-link relaxation (viscoelasticity).
Therefore strains measured many seconds after applying and holding a stress (during the solid
phase of the deformation process in Fig 5) will react as compressible viscoelastic solids.
Since we are applying a "known" stress and measuring the local strain, the bi-exponential curves
of strain increase over time measured at each pixel location (see Figs 5 – 7) is given by the
classical Kelvin-Voigt model (see Fig 7b and [6]). 0.5) and elastic. Small applied stresses ensure that the stress-strain curve is linear.
However if we hold the stress constant longer than a few seconds, we see that the strain
increases slowly over time (see plots in Fig 5). Whether we are imaging water-based gelatin
or breast tissue, it seems there are two physical mechanisms behind the mechanical relaxation.
These are related to fluid flow (poroelasticity) and cross-link relaxation (viscoelasticity).
Therefore strains measured many seconds after applying and holding a stress (during the solid
phase of the deformation process in Fig 5) will react as compressible viscoelastic solids.
Since we are applying a "known" stress and measuring the local strain, the bi-exponential curves
of strain increase over time measured at each pixel location (see Figs 5 – 7) is given by the
classical Kelvin-Voigt model (see Fig 7b and [6]).
|
|
 Fig 6.
The experiment for measuring mechanical relaxation [7] using a linear array is shown in Fig 6.
RF echo data are recorded up to 20 fps over a time as long as 100 s. Strain frames are computed
between adjacent RF frames to assemble a strain sequence. The mathematical equation predicting
strain from porous and viscous creep is given in by the model in Fig 7b. The appropriate equation
for time-varying strain is
Fig 6.
The experiment for measuring mechanical relaxation [7] using a linear array is shown in Fig 6.
RF echo data are recorded up to 20 fps over a time as long as 100 s. Strain frames are computed
between adjacent RF frames to assemble a strain sequence. The mathematical equation predicting
strain from porous and viscous creep is given in by the model in Fig 7b. The appropriate equation
for time-varying strain is
|
|

Fig 7a shows there are three terms result from a step stress stimulus. The first is These are illustrated in Fig 7a where, in this example, the inclusion is different from the background because of a higher collagen concentration. |
|
 Fig 7b. Fig 7b. |
|
 Fig 8 is taken from the work of Thomas Krouskop at Baylor Medical School. The
instantaneous slope approximates the elastic modulus for the incompressible phase of
the strain. The plot shows the intrinsic modulus contrast expected between different
types of tissues. In the incompressible phase, the strain is inversely proportional to
the elastic modulus. The plot also provides features important for designing clinical
imaging experiments. That is, the mechanical properties of breast tissues are nonlinear
for large compressions. However, linearity is reasonable to assume over small compressions,
e.g., 1% applied strain, if the tissue is preloaded to obtain the required contrast.
Fig 8 is taken from the work of Thomas Krouskop at Baylor Medical School. The
instantaneous slope approximates the elastic modulus for the incompressible phase of
the strain. The plot shows the intrinsic modulus contrast expected between different
types of tissues. In the incompressible phase, the strain is inversely proportional to
the elastic modulus. The plot also provides features important for designing clinical
imaging experiments. That is, the mechanical properties of breast tissues are nonlinear
for large compressions. However, linearity is reasonable to assume over small compressions,
e.g., 1% applied strain, if the tissue is preloaded to obtain the required contrast.
|
|
 1.B. Clinical Imaging and Interpretation
1.B. Clinical Imaging and Interpretation
Fig 9. We have been conducting human subject trials at UD Davis Medical Center with advice and guidance from Dr Karen Lindors MD, chief of the Breast Clinic. Examples are shown in Fig 9. Our patient population is different from other studies in that we select nonpalpable lesions from patients with suspicious mammograms that are undergoing US guided biopsy. We have pathological reports on each case to establish a diagnosis. Fig 9 shows three nonpalpable lesions that appear, left-to-right, stiffer (darker in strain) than the background, the same stiffness as the background, and softer (brighter in strain) than the background. Whereas palpable lesions are most often stiff, NP lesions can present with a variety of features. Does this finding lessen the value of elasticity imaging for breast lesion classification? I think not, but it does mean that we need more information to improve specificity. |
|
 Fig 10.
To do this, we first consider the basic anatomical structure of breast tissue in Fig 10.
We focus on the functional unit, the mammary lobule, and associated mammary duct.
Fig 10.
To do this, we first consider the basic anatomical structure of breast tissue in Fig 10.
We focus on the functional unit, the mammary lobule, and associated mammary duct.
|
|
 Fig 11.
From the milk duct illustrated in Figs 11-14, we review the molecular biology of
breast carcinoma as it affects ultrasonic interactions and associated mechanical properties.
Fig 11.
From the milk duct illustrated in Figs 11-14, we review the molecular biology of
breast carcinoma as it affects ultrasonic interactions and associated mechanical properties.
|
|
 Fig 12.
Many cancers begin as mutated luminal epithelial cells and remain as in situ disease,
Fig 12, until acted on by biochemical promoters.
Fig 12.
Many cancers begin as mutated luminal epithelial cells and remain as in situ disease,
Fig 12, until acted on by biochemical promoters.
|
|
 Fig 13.
As the cancerous cells outgrow their blood and nutrient supply, Fig 13, they send out chemical
signals to help them continue to grow. Many of these processes are controlled by signaling
molecules [11], but two processes are particularly important for our application. They are
the conversion of fibroblasts to myofibroblast that upregulate for collagen production within
the extracellular matrix (ECM). The stroma (loose connective tissue) is prepared during this
process in several ways. One way is to wall off the disease by growing a fibrous region around
the tumor – the desmoplastic reaction [11].
Fig 13.
As the cancerous cells outgrow their blood and nutrient supply, Fig 13, they send out chemical
signals to help them continue to grow. Many of these processes are controlled by signaling
molecules [11], but two processes are particularly important for our application. They are
the conversion of fibroblasts to myofibroblast that upregulate for collagen production within
the extracellular matrix (ECM). The stroma (loose connective tissue) is prepared during this
process in several ways. One way is to wall off the disease by growing a fibrous region around
the tumor – the desmoplastic reaction [11].
|
|
 Fig 14.
Desmoplasia is not well understood, but it is known to stiffen malignant tissues making then
palpable. Two other changes in the stroma are to (a) create an environment able to grow new blood
vessels – angiogenesis [12], and (b) reduce the number of fibronectin sites that epithelial cells
use to migrate [13]. The latter effect is thought to increase metastatic activity since cells
"lose their grip". Stromal changes that allow malignant breast disease to progress also
change the tissue ultrastructure in a manner that affects time-dependent mechanical properties.
To see this, let's focus in on the loose intralobular stromal region outlined by the box in the lower
right region of Fig 14.
Fig 14.
Desmoplasia is not well understood, but it is known to stiffen malignant tissues making then
palpable. Two other changes in the stroma are to (a) create an environment able to grow new blood
vessels – angiogenesis [12], and (b) reduce the number of fibronectin sites that epithelial cells
use to migrate [13]. The latter effect is thought to increase metastatic activity since cells
"lose their grip". Stromal changes that allow malignant breast disease to progress also
change the tissue ultrastructure in a manner that affects time-dependent mechanical properties.
To see this, let's focus in on the loose intralobular stromal region outlined by the box in the lower
right region of Fig 14.
|
|
 Fig 15.
There is a terrific paper by Stoeckelhuber et al [14] that describes the component structure of breast
stroma. In Fig 15 we see that the collagen fibers are surrounded by a polysaccharide gel. This gel
consists of strands of water-adsorbing proteoglycan molecules. Proteoglycans are a complex of
glycoaminoglycan (GAG) and protein that are bound to type I collagen fibers randomly positioned
in the stroma. GAGs contain sulfate groups dense with negative charge on the surface. The exposed
electric charge attracts polar water molecules to form structured water that is more viscous than bulk
water at the same temperature. During benign fibrotic lesion growth, when collagen density increases,
so does the density of proteoglycan molecules. The effect increases the viscosity of the polysaccharide
gel in breast stroma. So we expect fibrotic lesions to stiffen (lower strain) and the water-flow relaxation
time constant
Fig 15.
There is a terrific paper by Stoeckelhuber et al [14] that describes the component structure of breast
stroma. In Fig 15 we see that the collagen fibers are surrounded by a polysaccharide gel. This gel
consists of strands of water-adsorbing proteoglycan molecules. Proteoglycans are a complex of
glycoaminoglycan (GAG) and protein that are bound to type I collagen fibers randomly positioned
in the stroma. GAGs contain sulfate groups dense with negative charge on the surface. The exposed
electric charge attracts polar water molecules to form structured water that is more viscous than bulk
water at the same temperature. During benign fibrotic lesion growth, when collagen density increases,
so does the density of proteoglycan molecules. The effect increases the viscosity of the polysaccharide
gel in breast stroma. So we expect fibrotic lesions to stiffen (lower strain) and the water-flow relaxation
time constant 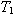 to increase. This is precisely what we see in
Fig 17, showing breast images from a patient
with a benign lesion. The variation in strain with time due to interstitial fluid movement is known as
poroelasticity. The mechanics of porous media was developed by Biot in a series of papers [15] beginning
in 1941 to describe soil consolidation under a load. These concepts have been expanded recently to modeling
[16] particularly of cartilage dynamics [17] and other biological tissues. to increase. This is precisely what we see in
Fig 17, showing breast images from a patient
with a benign lesion. The variation in strain with time due to interstitial fluid movement is known as
poroelasticity. The mechanics of porous media was developed by Biot in a series of papers [15] beginning
in 1941 to describe soil consolidation under a load. These concepts have been expanded recently to modeling
[16] particularly of cartilage dynamics [17] and other biological tissues.
|
|
 Fig 16.
Converesely, malignant processes, like infiltrating ductal carcinoma (IDC), develop a different
ultrastructure. The increase in collagen that can stiffen cancerous tissues is accompanied by a
reduction in proteoglycan density [18]. That reduces the viscosity of the fluid, Fig 16. Thus we
see a reduction in
Fig 16.
Converesely, malignant processes, like infiltrating ductal carcinoma (IDC), develop a different
ultrastructure. The increase in collagen that can stiffen cancerous tissues is accompanied by a
reduction in proteoglycan density [18]. That reduces the viscosity of the fluid, Fig 16. Thus we
see a reduction in 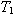 for malignant lesions as in Fig 18. Consequently, it appears to be helpful
to measure time-varying strain and the associated relaxation constant for malignant lesions as in Fig 18. Consequently, it appears to be helpful
to measure time-varying strain and the associated relaxation constant
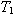 to clearly differentiate
malignant from benign lesions. to clearly differentiate
malignant from benign lesions.
|
|
 Fig 17. Fig 17. |
|
 Fig 18. Fig 18. |
|
 Fig 19.
The second relaxation mechanism, characterized by the time constant
Fig 19.
The second relaxation mechanism, characterized by the time constant 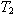 ,
is due to the relaxation of
hydrogen- and electrostaticaly-bonded cross-links within collagen fibers, Fig 19. Covalent
bonding between microfibrils is sparse in youth but increases slowly in organisms with age.
They are robust to mechanical and thermal stress and most other stimuli encountered in vivo.
The covalent bonds are most likely to be the source of the solid phase strain. That is, if we
let ,
is due to the relaxation of
hydrogen- and electrostaticaly-bonded cross-links within collagen fibers, Fig 19. Covalent
bonding between microfibrils is sparse in youth but increases slowly in organisms with age.
They are robust to mechanical and thermal stress and most other stimuli encountered in vivo.
The covalent bonds are most likely to be the source of the solid phase strain. That is, if we
let 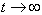 in (1), the strain becomes in (1), the strain becomes 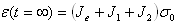 .
Strain is proportional to the sum of reactances [6] from each
component of the mechanical response. Note that the shear modulus in the solid phase is .
Strain is proportional to the sum of reactances [6] from each
component of the mechanical response. Note that the shear modulus in the solid phase is 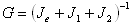 . However,
between the time that the step stress is applied and the strain reaches equilibrium, . However,
between the time that the step stress is applied and the strain reaches equilibrium, 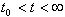 , the fragile
hydrogen-bonded cross-links are released to lower internal stresses. They will then reform but at
a lower energy state. We have begun examining this mechanism as a method for imaging
metabolically-driven changes in extracellular pH [19]. More on this later. , the fragile
hydrogen-bonded cross-links are released to lower internal stresses. They will then reform but at
a lower energy state. We have begun examining this mechanism as a method for imaging
metabolically-driven changes in extracellular pH [19]. More on this later.
|
|
|
1.C Gelatin as a Physical Model for Imaging Development
Pure, natural gelatin is collagen. Formation begins as polypeptide fragments of a few types of amino acids (three most common are glycine, proline, and hydroxyprolin, Fig 18). The fragments are joined through peptide linkages to assemble into a triple helix structure [20]. When added to water at the correct temperature and concentration, it forms a gel. Commercially available gelatin powder is produced from denatured collagen derived, in most common uses, from fibrous animal tissues like skin [21]. Impure forms of gelatin, including commercial lab-grades, are distinguishable as gelatine. Like breast stroma, gelatin contains mostly type I collagen molecules, but few fibers are formed in network. The network is a hydrocolloid (water-loving) material that absorbs up to 10 times its mass in water. Unlike stromal tissue, in vivo, there is no polysaccharide gel surrounding the collagen fibers. The few fibers that form are shorter in length depending on pH, temperature history and other environmental factors, and the cross-linking is less robust than that in vivo. Nevertheless, gelatinous collagen fibers expose electrically charged sites that adsorb and structure water in a manner similar to the polysaccharide gels in tissue. Also aldehydes and other chemical cross-linking agents are used to temporally and thermally stabilize the colloid structure. Like connective tissues, in vivo, the number of covalent bonds between collagen fibers in gelatin increase as the gel ages. There is literature on the shear and bulk elastic properties of gelatin used to develop ultrasound phantoms for medical imaging applications from group at University of Wisconsin and elsewhere [22-24]. However, the study of poro- and viscoelastic responses is predominantly in the vast literature on food sciences and medical prosthetic devices. Gelatin is usually produced from a process that denatures collagenous biomaterials by treatment with alkali or acidic solutions [20,21]. Type A gelatin uses acidic processing, and type B gelatin uses alkali processing. Gelatin type is extremely important if you are interested in time-varying mechanical responses, because type determines the isoelectric point. The isoelectric point (IEP) of a gel is the pH of a solution containing gelatin proteins whereby the following measurement properties are all minimized: movement of particles in an electric field, conductivity, solubility, osmotic pressure, swelling, and viscosity [25]. In short, IEP is the pH where the gel is least reactive (most stable) with respect to the measurements listed above. This is not to be confused with the isoionic point (IIP) [25], which is defined as the pH of a solution for which the addition of gelatin causes no change in the pH value of the solution.1 If the gelatin is pure collagen protein and not gelatine, as are most lab-grade products, then IEP = IIP. In that special case, IIP is the pH of a solution where there is no net charge on the surface of the collagen fibers [21]. IIP for acid-precursor gelatins (type A) is in a pH range of 9.0-9.2, similar to native collagen [20]. IIP for alkali-precursor gelatins (type B) is in a pH range of 4.8 – 5.2. However IEP can be most anywhere on the pH scale; the density of charged sites depends in how the gelatin was prepared and its purity. Gelatin viscosity will double as the net molecular charge per collagen molecule increases from 0 at IEP to ±30 (see Fig II-30 in [20]). 1 There seem to be an endless supply of definitions for IEP and IIP, and, not being a biochemist, I am unsure how to interpret most of them. For pure clarity of prose, I prefer the discussion by Adair from 1937 [25]. |
|
|
References:
[1] Chaturvedi P, Insana MF, Hall TJ: 2-D companding for noise reduction
in strain imaging. IEEE Trans. Ultrason. Ferro. Freq. Contrl.
UFFC-45:179-191, 1998. |





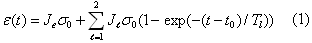
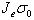 and is constant with
time; it describes strain during the incompressible phase, before relaxation can occur. When measurement
time
and is constant with
time; it describes strain during the incompressible phase, before relaxation can occur. When measurement
time 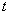 is very close to the time that the stress was applied
is very close to the time that the stress was applied 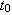 , then
, then
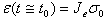 . This is the quantity we normally
think of as a strain image in static elasticity imaging. The second two terms in (1) grow in amplitude
over time. The amount of growth depends on the elastic constants
. This is the quantity we normally
think of as a strain image in static elasticity imaging. The second two terms in (1) grow in amplitude
over time. The amount of growth depends on the elastic constants 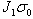 and
and
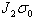 , and the corresponding rates of
growth are characterized by time constants
, and the corresponding rates of
growth are characterized by time constants 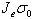 ,
,