Insana Lab: Ultrasonic Imaging - The University of Illinois at Urbana-Champaign
Project 5: Efficient Ultrasonic Beamforming Strategies: Spatial Filtering
Kang-Sik Kim [kangsik@illinois.edu]
 Fig 1.
Focusing (or beamforming) is one of the most important factors
in determining the image quality of ultrasound B-mode images [1-8]. Currently, most
ultrasound systems employ different focusing methods on transmit and receive. On transmit,
the focal length is often fixed, and therefore the best spatial/contrast resolution is near
the transmit focal length. Lateral resolution is degraded in the near-field and far-field.
On the other hand, delaying and summing echo samples from receive channels dynamically
allows us to focus receive echo signals at every depth; the method is called dynamic
receive focusing (DRF) [2-7]. Overall B-mode image quality and resolution are affected
by both transmit and receive focusing whose performance is represented by beam patterns as in Fig 1.
Fig 1.
Focusing (or beamforming) is one of the most important factors
in determining the image quality of ultrasound B-mode images [1-8]. Currently, most
ultrasound systems employ different focusing methods on transmit and receive. On transmit,
the focal length is often fixed, and therefore the best spatial/contrast resolution is near
the transmit focal length. Lateral resolution is degraded in the near-field and far-field.
On the other hand, delaying and summing echo samples from receive channels dynamically
allows us to focus receive echo signals at every depth; the method is called dynamic
receive focusing (DRF) [2-7]. Overall B-mode image quality and resolution are affected
by both transmit and receive focusing whose performance is represented by beam patterns as in Fig 1.
As shown in left panel of Fig. 1, conventional dynamic focusing (CDF) provides the best pulse-echo spatial resolution near the transmit focal depth. Therefore to further improve the resolution of current ultrasound imaging, it is necessary to overcome the limitation of the fixed transmit focusing. The goal of this research project is to develop efficient 2-way dynamic focusing methods. |
|
 Fig 2 shows lateral beam patterns at the focal depth
Fig 2 shows lateral beam patterns at the focal depth 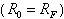 and in the far field for
continuous-wave transmission. The beam width is just the Fourier transform of the aperture function and in the far field for
continuous-wave transmission. The beam width is just the Fourier transform of the aperture function
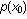 provided we can eliminate the quadratic phase term, provided we can eliminate the quadratic phase term,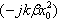 , which degrades resolution. Focusing
eliminates this quadratic phase term, such that the rectangular aperture of a linear array is expressed
by sinc(x) function. The goal of focusing (bamforming) is to eliminate the quadratic phase term. , which degrades resolution. Focusing
eliminates this quadratic phase term, such that the rectangular aperture of a linear array is expressed
by sinc(x) function. The goal of focusing (bamforming) is to eliminate the quadratic phase term.
|
|
 Fig 3 illustrates pulse echo beam patterns from conventional dynamic focusing
methods. In the near or far field, the beam pattern has high side lobe levels that reduce
image contrast. Near the transmit focal length, the pulse echo beam pattern attains the
diffraction limit on spatial resolution, limited by the frequency of the sound waves and
aperture size. Mathematically, the narrowest-possible linear array beam pattern is given
by sinc2
Fig 3 illustrates pulse echo beam patterns from conventional dynamic focusing
methods. In the near or far field, the beam pattern has high side lobe levels that reduce
image contrast. Near the transmit focal length, the pulse echo beam pattern attains the
diffraction limit on spatial resolution, limited by the frequency of the sound waves and
aperture size. Mathematically, the narrowest-possible linear array beam pattern is given
by sinc2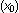 function, but this occurs only in the narrow range known as the depth of focus.
The goal is to implement diffraction limited beam patterns at all image depths. function, but this occurs only in the narrow range known as the depth of focus.
The goal is to implement diffraction limited beam patterns at all image depths.
|
|
 Fig 4 describes the spatial matched filter (SMF) beamformer mathematically and
graphically. Spatial matched filters focusing the beam instead without the use of the conventional
delay-and-sum operation. Applying SMF to echoes from unfocused beams allows us to approximate
diffraction-limited imaging conditions at all depths, with some loss of axial resolution. SMF
beamforming can be considered as an alternative to CDF.
Fig 4 describes the spatial matched filter (SMF) beamformer mathematically and
graphically. Spatial matched filters focusing the beam instead without the use of the conventional
delay-and-sum operation. Applying SMF to echoes from unfocused beams allows us to approximate
diffraction-limited imaging conditions at all depths, with some loss of axial resolution. SMF
beamforming can be considered as an alternative to CDF.
|
|
 Fig 5.
To implement the SMF beamformer, we transmit ultrasound waves using a large
transmit aperture with a fixed focal length. RF images are formed from each receive channels. The
transmit and receive beam patterns are expressed as shown in Fig. 5 where x1 represents the lateral
location of each receive element.
Fig 5.
To implement the SMF beamformer, we transmit ultrasound waves using a large
transmit aperture with a fixed focal length. RF images are formed from each receive channels. The
transmit and receive beam patterns are expressed as shown in Fig. 5 where x1 represents the lateral
location of each receive element.
|
|
 Fig 6.
Next, a spatial matched filter is applied to each RF image and summed.
Filtering aligns the individual channel images so that delay circuits are unnecessary.
This method can provide two-way focused beam pattern at all imaging depths regardless of
transmit focal depth.
Fig 6.
Next, a spatial matched filter is applied to each RF image and summed.
Filtering aligns the individual channel images so that delay circuits are unnecessary.
This method can provide two-way focused beam pattern at all imaging depths regardless of
transmit focal depth.
|
|
 Fig 7 is a block diagram of the proposed SMF method using impulse-response
results to show the effects at each stage.
Fig 7 is a block diagram of the proposed SMF method using impulse-response
results to show the effects at each stage.
|
|
 Fig 8.
Continuous-wave (CW) beam patterns from simulations of
linear array fields via Field II are shown to illustrate SMF method and compare it
with CDF method. We used a 10 MHz array with 96 transmit and receive channels. The
fixed transmit focal length was 40 mm. No apodization was applied. The label
"Focus" indicates diffraction limited pulse-echo beam patterns, the gold
standard for comparisons. The label "CDF" indicates conventional dynamic
focusing was applied. The label "SMF" indicates the spatial matched
filter beamformer was applied. It shows nearly the same beam pattern as Focus at
all imaging depth regardless of the transmit focal depth. SMF improves the lateral
resolution as compared with DRF.
Fig 8.
Continuous-wave (CW) beam patterns from simulations of
linear array fields via Field II are shown to illustrate SMF method and compare it
with CDF method. We used a 10 MHz array with 96 transmit and receive channels. The
fixed transmit focal length was 40 mm. No apodization was applied. The label
"Focus" indicates diffraction limited pulse-echo beam patterns, the gold
standard for comparisons. The label "CDF" indicates conventional dynamic
focusing was applied. The label "SMF" indicates the spatial matched
filter beamformer was applied. It shows nearly the same beam pattern as Focus at
all imaging depth regardless of the transmit focal depth. SMF improves the lateral
resolution as compared with DRF.
|
|
 Fig 9 shows the point spread function (PSF) for each
of the three methods using a pulsed transducer excitation. The bandwidth of the pulse is 70% of the
center frequency. SMF method provides almost the same PSF as Focus at 40 mm and 60 mm. However the
PSF of SMF is slightly inferior to Focus because 2-D spatial matched filters were used for
constructing 2-D images while 1-D spatial matched filters were used in the previous CW case.
Despite of this difference, SMF provides improved resolution in the near-field and far-field
compared with CDF.
Fig 9 shows the point spread function (PSF) for each
of the three methods using a pulsed transducer excitation. The bandwidth of the pulse is 70% of the
center frequency. SMF method provides almost the same PSF as Focus at 40 mm and 60 mm. However the
PSF of SMF is slightly inferior to Focus because 2-D spatial matched filters were used for
constructing 2-D images while 1-D spatial matched filters were used in the previous CW case.
Despite of this difference, SMF provides improved resolution in the near-field and far-field
compared with CDF.
|
|
 Fig 10 displays computer simulated cyst phantom images using the three beamforming
methods. SMF provides comparable images to Focus (gold standard) at 40 mm (transmit focal length)
and 60 mm (far field). However, in the near field, like the PSF result of Fig 9, the spatial resolution
and contrast to noise ratio (CNR) of SMF image is slightly degraded compared with Focus. Compared with
CDF, SMF image quality is significantly improved in the near and far fields.
Fig 10 displays computer simulated cyst phantom images using the three beamforming
methods. SMF provides comparable images to Focus (gold standard) at 40 mm (transmit focal length)
and 60 mm (far field). However, in the near field, like the PSF result of Fig 9, the spatial resolution
and contrast to noise ratio (CNR) of SMF image is slightly degraded compared with Focus. Compared with
CDF, SMF image quality is significantly improved in the near and far fields.
|
|

Fig 11. Other simulations were performed to compare the performance between CDF and SMF in the presence of a planar phase aberrator. All images are of a cyst positioned in the transmit-aperture near field. Images on the left were constructed w/o phase aberration, while those on the right were constructed w/ phase aberration. The rms aberration amplitude is 34 ns and the spatial correlation length along the lateral dimension is 3.6mm. These are typical values for breast tissue. With phase aberration, image resolution is degraded significantly with both CDF and SMF methods, but the image quality of the SMF image is superior to CDF. Both methods are equally sensitive to phase aberration. |
|

Fig 12. We images the point spread functions from a 10 MHz, f/1.5, 60% BW, 45 mm diameter, annular array (8 rings) to verify performance experimentally. PSF in the near field (25 mm), at the transmit focal depth (45 mm), and in the far field (65 mm) are shown. The target was a wire phantom in water. |
|

Fig 13 compares the SMF method applied to individual channels (before BF) versus that applied to beamformed RF echo signals (after BF). Although the latter method is simpler and faster, filtering individual channels generates superior image quality because of lower side lobes. Using apodization to reduce the side lobe level is effect at the cost of main lobe width (spatial resolution). |
|

Fig 14. SMF is well suited to high frequency imaging with array, where delay circuits for dynamic focusing are difficult to implement. To evaluate the performance of spatial filtering method on beamformed data for high frequency application, PSF simulations were generated. We assumed a circular aperture, 70 MHz transducer with 45% BW, 4.66 mm diameter and 7 mm focal depth (f/1.5). The figure displays the PSFs from a fixed geometric focus and SMF method six depths. SMF provides a more improved beam except at the 7 mm focal length. |
|
|
References:
[1] A. Macovski, Medical Imaging Systems, Prentice Hall, pp. 73-224, 1983. |




