Insana Lab: Ultrasonic Imaging - The University of Illinois at Urbana-Champaign
Project 3: Vascular Wall Shear Rate (WSR) Measurements Using Ultrasound
5.5.05
 2.A. Why Measure WSR? The Medical Problem.
2.A. Why Measure WSR? The Medical Problem.Fig 1. There is an extensive literature on the role of environmental factors and vascular endothelial cells (ECs) in the formation of arterial plaques and cardiovascular diseases (CVD) [2-7]. The following very brief (and simplistic) view of important CVD factors is meant to motivate the reader in the need for wall shear rate measurements. Our approach to this measurement is described below. As we age, the protective EC barrier is less effective and easily damaged, Fig 1 (above). Damage is accelerated in individuals that smoke, have poor diets, maintain stressful lifestyles (like professors) and are subjected to other adverse environmental factors. Under these conditions, the EC barrier breaks down and the endothelial cells change to an atherogenic phenotype: they release more vasoconstrictors than vasodilators, and vascular smooth muscle cells from the media proliferate to invade the intimal layer. Importantly, changes in the activity of adhesion molecules (e.g., ICAM-1 and VCAM-1) located on the EC surface is one inflammatory response to the damage [8]. These ligands capture monocytes circulating in the blood, pulling them into the intima where they differentiate into macrophages. Macrophages then combine with circulating low-density lipids (LDLs) that enter the wall through the leaky EC barrier to become foam cells that form the lipid pool of the arterial plaque. Adhesion molecules are expressed in regions of the vasculature where the wall shear stress (WSS) is low and oscillatory [9]. The role of adhesion molecules in plaque formation is usually studied in flow chambers using cell cultures rather than in animal models or patients, in vivo. Our goal is to adapt ultrasonic methods for accurate measurements of wall shear rate, in vivo, to describe how temporal and spatial variations influence atherosclerosis. |
|
 Fig 2.
WSS is the product of wall shear rate (WSR) and blood viscosity. Fig 2.
Also WSR is related to blood velocity V via the radial derivative
Fig 2.
WSS is the product of wall shear rate (WSR) and blood viscosity. Fig 2.
Also WSR is related to blood velocity V via the radial derivative 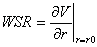 where and r is the radial position in the vessel. The derivative is evaluated at the wall surface
where r = r0. Since the velocity is zero outside the lumen, the function is not continuously
differentiable at least in theory. Fig 2 shows that the velocity profile for parabolic
laminar flow (red line) and the average measurement (blue line). Because of the finite
ultrasonic pulse length and other spatial averaging processing parameters used in Doppler
velocity estimation, the percent velocity error is largest near the wall. So WSR estimates
are biased. If you also consider that measurement noise is amplified by the derivative,
the total WSR errors can be very large. Jean Tsou in the lab estimated the errors using
a flow phantom and 5-cycle color-flow Doppler pulse. She found that WSR estimates are
biased -28% at 100 mm/s flow velocity, and the corresponding relative standard deviation
is 15%. Accurate WSS estimates for vascular EC function investigations depend entirely
on our ability to accurately estimate velocity near the lumen wall.
where and r is the radial position in the vessel. The derivative is evaluated at the wall surface
where r = r0. Since the velocity is zero outside the lumen, the function is not continuously
differentiable at least in theory. Fig 2 shows that the velocity profile for parabolic
laminar flow (red line) and the average measurement (blue line). Because of the finite
ultrasonic pulse length and other spatial averaging processing parameters used in Doppler
velocity estimation, the percent velocity error is largest near the wall. So WSR estimates
are biased. If you also consider that measurement noise is amplified by the derivative,
the total WSR errors can be very large. Jean Tsou in the lab estimated the errors using
a flow phantom and 5-cycle color-flow Doppler pulse. She found that WSR estimates are
biased -28% at 100 mm/s flow velocity, and the corresponding relative standard deviation
is 15%. Accurate WSS estimates for vascular EC function investigations depend entirely
on our ability to accurately estimate velocity near the lumen wall.
|
|
 Fig 3.
Given the challenges imposed by the measurement environment listed in Fig 3, we are
pursuing the following solution. We use broadband imaging pulses and cross-correlation
displacement estimators to measure velocity [10,11]. These features yield a potential
to provide higher spatial and temporal resolution than color flow or pulsed Doppler
approaches, but they suffer from relatively low echo signal-to-noise ratio (eSNR).
So we are also investigating applications of temporally coded pulse excitation.
Fig 3.
Given the challenges imposed by the measurement environment listed in Fig 3, we are
pursuing the following solution. We use broadband imaging pulses and cross-correlation
displacement estimators to measure velocity [10,11]. These features yield a potential
to provide higher spatial and temporal resolution than color flow or pulsed Doppler
approaches, but they suffer from relatively low echo signal-to-noise ratio (eSNR).
So we are also investigating applications of temporally coded pulse excitation.
|
|
 2.C. Coded Excitation for Velocity Estimation.
2.C. Coded Excitation for Velocity Estimation.Fig 4. Coded excitation, Fig 4, is used to increase the time average pulse energy without increasing the instantaneous spatial-peak intensity. We transmit in time an extended pulse sequence into the body and then filter the echoes to restore spatial resolution. We have been investigating coded pulse excitation for strain imaging applications [12], and are extending that study for WSR estimation. |
|
 Fig 5.
The cross correlation velocity estimator is summarized in Fig 5. We record two-waveform broadband
ensembles at each position. The component of the displacement vector along the beam axis is found
from the cross correlation estimate
Fig 5.
The cross correlation velocity estimator is summarized in Fig 5. We record two-waveform broadband
ensembles at each position. The component of the displacement vector along the beam axis is found
from the cross correlation estimate 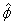 . Displacement is the value of the argument d that minimizes
the objective function given in the figure. The first term depends only of the data, while the
second term is a smoothness penalty function. dfit is the displacement obtained by fitting the
color-flow velocity profile to a laminar (second-order) or blunt-flow (higher-order) model function,
subject to the constraint that the velocity is zero at the wall. . Displacement is the value of the argument d that minimizes
the objective function given in the figure. The first term depends only of the data, while the
second term is a smoothness penalty function. dfit is the displacement obtained by fitting the
color-flow velocity profile to a laminar (second-order) or blunt-flow (higher-order) model function,
subject to the constraint that the velocity is zero at the wall.  = 0.6 is an adjustable constant.
From the displacement estimate = 0.6 is an adjustable constant.
From the displacement estimate 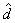 , velocity is estimated as shown at the bottom of Fig 5. , velocity is estimated as shown at the bottom of Fig 5.
|
|
 Fig 6 shows the estimation procedure using a linear system model. Phase-modulated codes c(t)
are convolved with a discrete base sequence b(t) to generate the electrical waveform e(t) that
drives the transducer h(x, t). The tissue f(x,t) is scanned twice, where the time interval
between the two pulse-echo waveforms depends on the blood velocity. Since we’re not using
Fourier techniques, aliasing is not a problem in the traditional sense. Nevertheless, the
echo waveform pair must remain coherent, which means the waveform interval must be short
enough so that many of the scatterers remain in the pulse volume between recordings. The
echo waveforms are decoded (compressed) using digital filters, the resulting echoes are
preprocessed using an equalization algorithm [11] before WSR is estimated. The results
are evaluated using relative bias and standard deviation as defined in Fig. 6.
Fig 6 shows the estimation procedure using a linear system model. Phase-modulated codes c(t)
are convolved with a discrete base sequence b(t) to generate the electrical waveform e(t) that
drives the transducer h(x, t). The tissue f(x,t) is scanned twice, where the time interval
between the two pulse-echo waveforms depends on the blood velocity. Since we’re not using
Fourier techniques, aliasing is not a problem in the traditional sense. Nevertheless, the
echo waveform pair must remain coherent, which means the waveform interval must be short
enough so that many of the scatterers remain in the pulse volume between recordings. The
echo waveforms are decoded (compressed) using digital filters, the resulting echoes are
preprocessed using an equalization algorithm [11] before WSR is estimated. The results
are evaluated using relative bias and standard deviation as defined in Fig. 6.
|
|
 Fig 7.
The experimental setup is shown in Fig 7.
Fig 7.
The experimental setup is shown in Fig 7.
|
|
 Fig 8.
Results using two uncoded (analog broadband and narrowband sinusoidal pulses) and two coded pulses
(digital FM chirp and PM Optimal code [12]) are summarized in Figs 8-11. Thus far we only have
measurement in a flow phantom using a lab system described in [10-13]. In Fig 8,
we see broadband pulse-echo impulse responses imaged over a range of depths for a 10 MHz
annular array. The geometric aperture is f/1.5, and so the depth of focus is only 2.4 mm –
perfect for studying variable eSNR regions, since eSNR is high only near the focal length.
To the right in Fig 8, we see impulse response (IR) functions at the focal length for the
four test pulses. The amplitudes of the IR functions for the decoded chirp and Optimal
pulses were displayed in compressed grayscale to show range side lobes. In the bottom
half of Fig 8, the eSNR values are shown for four pulses compressed using Wiener and
matched filters in the focal zone and far field. eSNR is found from the object and
noise variances,
Fig 8.
Results using two uncoded (analog broadband and narrowband sinusoidal pulses) and two coded pulses
(digital FM chirp and PM Optimal code [12]) are summarized in Figs 8-11. Thus far we only have
measurement in a flow phantom using a lab system described in [10-13]. In Fig 8,
we see broadband pulse-echo impulse responses imaged over a range of depths for a 10 MHz
annular array. The geometric aperture is f/1.5, and so the depth of focus is only 2.4 mm –
perfect for studying variable eSNR regions, since eSNR is high only near the focal length.
To the right in Fig 8, we see impulse response (IR) functions at the focal length for the
four test pulses. The amplitudes of the IR functions for the decoded chirp and Optimal
pulses were displayed in compressed grayscale to show range side lobes. In the bottom
half of Fig 8, the eSNR values are shown for four pulses compressed using Wiener and
matched filters in the focal zone and far field. eSNR is found from the object and
noise variances, 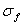 and and 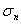 using using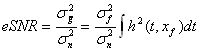 . .The chirp and optimal codes with matched-filter compression give the highest eSNR gain. However that is not the whole story. Range lobes degrade performance as well as low eSNR. |
|
 Fig 9.
The effect on WSR errors as a function of eSNR is shown in Fig 9. The data shows us
that coded excitation can only be helpful at low eSNR, i.e., when eSNR < 30 dB.
Fig 9.
The effect on WSR errors as a function of eSNR is shown in Fig 9. The data shows us
that coded excitation can only be helpful at low eSNR, i.e., when eSNR < 30 dB.
|
|
 Fig 10 shows that the lowest WSR errors are found for the optimal code and that the results
are only weakly dependent on the average flow velocity.
Fig 10 shows that the lowest WSR errors are found for the optimal code and that the results
are only weakly dependent on the average flow velocity.
|
|
 Fig 11 gives the spatial distribution of errors for three pulse types.
Fig 11 gives the spatial distribution of errors for three pulse types.
|
|

Fig 12 shows that we need to answer another question before we can say whether our velocity estimator for WSR measurements is of any value for biological investigations. We are lowering measurement errors but are they low enough to make a difference? We need to know the relationship between errors in WSR estimates and differences in EC function. For example, if reduction in WSR errors from 20% to 10% allows us to see much greater differences in EC function, then our signal processing improvements are helpful. For these investigations, Jean Tsou is working with Scott Simon at UC Davis to develop a flow chamber in which EC are grown and where the WSR values are precisely known. Jean worked with Abdul Barakat at UC Davis to model the velocity in the PDMS chamber using computational fluid dynamics (CFD) software. They found that a linear WSR region with an adjustable slope is possible to develop (lower right). This unique phantom design, involving live EC, could help us answer the basic questions. |
|
|
References:
[1] Weinbaum S, Zhang X, Han Y, Vink H, Cowin SC: Mechanotransduction
and flow across the endothelial glycocalyx, Proc Natl Acad Sci U S A. 100:7988-95, 2003 |




