Insana Lab: Ultrasonic Imaging - The University of Illinois at Urbana-Champaign
Project 2: Measuring and Modeling Viscoelastic Behavior
Mallika Sridhar Keralapura [msridhar@ucdavis.edu]
Fig 1a shows the basic formulation used from linear theory to represent
viscoelastic behavior of soft, tissue-like media such as water-based polymers
and connective tissues. The constitutive equation (relating stress to strain)
is obtained by applying Boltzmann superposition principle to Hookes’s Law (Eq 1)
[Fung 93], where 'C' is a compliance tensor that all describes material properties.
The convolution of Eq (1) indicates that strain at time t depends on a weighted
sum of stresses at an earlier times for a system initially at rest. Using the
Laplace representation of Eq (1), the strain expression can be simplified to
represent fundamental properties such as shear and bulk moduli if we are able
to assume isotropy (Eq 2). We can combine the two fundamental moduli into one
derived modulus: elastic compliance modulus.
|
|
|
Fig 1b.
The elastic compliance can be modeled (Eq 3) using a standard discrete
Kelvin model [Fung 93]. By substituting Eq (3) into Eq (2) and taking the inverse
Laplace transform to work in the time domain, a model for time varying strain can
be obtained (Eq 4). It provides measurement parameters that are related to
fundamental properties of the medium. The last term in braces indicates pure viscous losses. |
|
Fig 2.
We use a number of ways to measure viscoelastic properties of tissue-mimicking
gelatin hydrogels. Fig 2 shows 4 custom setups. Fig 2a is used to apply a uniaxial stress
or strain to the sample. A stress relaxation experiment (constant strain, record time
varying force or stress) or creep experiment (constant stress, record time varying
displacement or strain) can be performed. We also use this setup to image spatially
varying viscoelastic properties of gelatin samples by attaching a linear array ultrasound
transducer to the compression plate. Creep can be measured in shear using a cone
viscometer Fig 2b, i.e., only a shear stress can be applied. Another deformation we
commonly use is confined uniaxial compression, where the sample is placed in a syringe
as shown in Fig 2c. By confining the gel, we can separate in time the fluid redistribution
from network based relaxation. This has proved to be an efficient way to study underlying
mechanisms in gelatin that give rise to its viscoelastic effects. Other groups use similar
setups to study mechanisms in collagen hydrogels [Chandran 04]. We also use indentation
techniques adapted by [Kargel 01], to efficiently measure elastic properties of the samples
using the setup shown in Fig 2d. This method takes into consideration the effects of sample
geometry, boundary conditions, material conditioning, and viscous responses. As a result,
a combination of these measurements on gelatin either in shear, uniaxial unconfined or
confined can be used to validate gelatin viscoelastic properties. One must take care
while comparing the estimates obtained from one experiment to the other (see [Ferry]
for details).
|
|
Fig 3.
(a) Creep experiment under compressive load and (b) under shear load. One of the first
tests performed on all viscoelastic creep data was to determine if the viscous term was present
as indicated by the braces in Eq (4). Data obtained from the viscometer at 2 stress levels of 3
and 30 Pa clearly illustrates that the presence of terminal flow is stress dependent, i.e.,
there exists a stress threshold beyond which the flow is present (see rheodictic curve in Fig 3b).
At low stress levels of 3 Pa, a transition region is followed by a steady state region
(nonrheodictic curve in Fig 3b) . No steady or equilibrium state is seen at higher stresses.
When rheodictic behavior is seen, a initial transition region is followed by a steady state
region whose value is 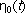 . Arrheodictic behavior is tough to visualize with any other
deformation. Rheodictic behavior is more difficult to see for creep under a uniaxial
compressive stress, Fig 3a.
|
|
|
Fig 4.
Before making detailed measurements on gelatin gels, we needed to consider which parameters
are involved in the measurement. For instance, how much compression has to be applied to the sample
for it to respond linearly? To answer that question, the measurement in Fig 2a can be used to apply
oscillatory displacements to gelatin samples and corresponding forces can be recorded. A plot of
stress Vs strain shown in Fig 4 can identify regions where stress varies linearly with strain, i.e.,
the assumed models are valid. Furthermore, these curves can help determine how much strain needs to
be applied to samples of different stiffness or gel concentrations to maintain approximately the same
stress and yet elicit linear behavior when comparisons need to be made. It can also be used to estimate
the elastic moduli of samples.
|
|
|
Fig 5.
We asked: How long should we acquire data and at what rate in order to accurately measure
the frequency spectrum of creep data. The temporal sampling frequency (i.e., the ultrasonic frame rate)
determines the highest strain frequencies that can be measured without aliasing. The total acquisition
time determines the frequency interval of the spectrum and the lowest measurable frequency. A imaginary
part of the one-sided Fourier transform of the creep curve is shown in Fig 5a. This simulated spectrum
assumes no noise and a bi-exponential model (L=2). Note: Although the relaxation times in the example
are nearly two orders of magnitude different, the peaks overlap significantly. Distinguishing high-frequency
peaks in the strain spectrum is difficult. We show in Fig 5b the spectral response obtained when gelatin is
sheared in the cone viscometer. Looking at the spectrum, it is clear that we sample fast enough and acquire
long enough to obtain the entire bandwidth of the signal.
|
|
|
Fig 6.
Until now, all equations were derived under the assumption of a step stress stimulus. In practice
only a ramp-and-hold stimulus can be applied. We also develop the equations using a ramp stimulus and
investigated its effect using simulated data. The spectral response shown in Fig 6 shows that by increasing
the time to apply the stimulus, the position of the spectral peak remains unchanged but its associated
amplitude is dampened. As a result, if we are interested only in time constants, the step stimulus equation
is acceptable to use. Furthermore it saves more than a factor of two in computational time.
|
|
|
Fig 7.
To better understand viscoelastic mechanisms, measurements were made on gelatin in a
confined state. Fig 7a shows examples of normalized stress relaxation data
obtained from such an experiment. Measured frequency spectra from gelatin are shown in
Fig 7b. We see one prominent spectral peak at 1.05 rad/s. One of the first
points to note is that the sample was operating in its linear range. Spectra obtained at
5% and 2% strains scaled in amplitude appropriately and were associated with unchanged
spectral peaks. Furthermore, the spectral peak position did not change significantly
when ramp and hold loading was used, but was associated with a decrease in amplitude.
This could be due to the long ramp time during which mechanisms already begin to engage.
A 5% step strain response was attenuated slightly when the measurement was repeated 4
days after congealing. This could be due to the continued cross-linking that occurs over
time in the gel that impedes water flow. We also noted that by decreasing the sample
length to 5mm, the amplitude of the mechanisms was significantly decreased. This was
also noted by [4]. In confined compression, the other mechanism, i.e., network based
relaxation occurs after fluid flow effects. It is not particularly visible as another
prominent peak in the spectra but it occurs at longer times and is associated with a
broad bandwidth.
|
|
|
References:
[1] J. Ferry, Viscoelastic Properties of Polymers. New York:
John Wiley and Sons, 1961. |